Grasping Data Relationships: A Primer on Data Dispersion
Data dispersion, in the context of statistical analysis and machine learning, refers to the extent to which numerical data points are scattered or spread out. Understanding data dispersion is crucial because it provides insights into the variability and relationships within a dataset. It quantifies how much variables change in relation to one another, influencing the accuracy and reliability of statistical models. Recognizing these relationships enables drawing meaningful conclusions and making informed decisions based on the data. One common method to describe this relationship is through the calculation of the covariance of a matrix python. The concept helps determine if the relationship is positive (variables increase or decrease together) or negative (variables move in opposite directions).
The importance of data dispersion extends to various fields, including finance, economics, and engineering. For example, in finance, understanding the covariance of a matrix python between different assets in a portfolio is essential for risk management and portfolio optimization. In machine learning, analyzing the covariance of a matrix python between features can aid in feature selection and dimensionality reduction. Properly understanding and calculating data dispersion, especially the covariance of a matrix python, is the first step towards more advanced analytical techniques.
Covariance is a statistical measure that indicates the extent to which two variables change together. A positive covariance indicates that the two variables tend to increase or decrease together, while a negative covariance suggests they tend to move in opposite directions. Calculating the covariance of a matrix python is a fundamental step in assessing the linear relationship between variables. This allows you to understand how changes in one variable might relate to changes in another and is crucial for making predictions and informing decisions, making the covariance of a matrix python a powerful tool.
NumPy’s Power: How to Calculate Data Dispersion Using NumPy
NumPy is a cornerstone of numerical computing in Python. It offers powerful tools for array manipulation and mathematical operations. Its efficiency makes it ideal for calculating data dispersion. This section provides a step-by-step guide on using NumPy’s `cov()` function. We will calculate the covariance of a matrix python, showcasing NumPy’s capabilities.
To begin, import the NumPy library: `import numpy as np`. Next, create a sample dataset as a NumPy array. For example: `data = np.array([[1, 2, 3, 4, 5], [2, 4, 6, 8, 10]])`. This creates a 2×5 array. Each row represents a variable, and each column represents an observation. To calculate the covariance matrix, use the `np.cov()` function: `covariance_matrix = np.cov(data)`. By default, `np.cov()` treats each row as a variable. If your data is arranged with variables in columns, set the `rowvar` argument to `False`: `covariance_matrix = np.cov(data, rowvar=False)`. This is crucial for obtaining the correct covariance of a matrix python.
The `np.cov()` function returns the covariance matrix. This matrix describes the relationships between the variables in your dataset. The diagonal elements represent the variances of each variable. The off-diagonal elements represent the covariances between pairs of variables. A positive covariance indicates that the variables tend to increase or decrease together. A negative covariance suggests they move in opposite directions. For instance, in the example above, `covariance_matrix[0, 1]` (or `covariance_matrix[1, 0]`) shows the covariance between the first and second variables. Understanding how to calculate the covariance of a matrix python using NumPy provides a solid foundation for more advanced statistical analysis. Remember that the magnitude of the covariance is scale-dependent. It’s not directly comparable across different datasets without normalization. NumPy’s `cov()` function is a fundamental tool. It is essential for understanding data relationships and performing various data analysis tasks.
Decoding the Data Dispersion Matrix: Interpreting the Results
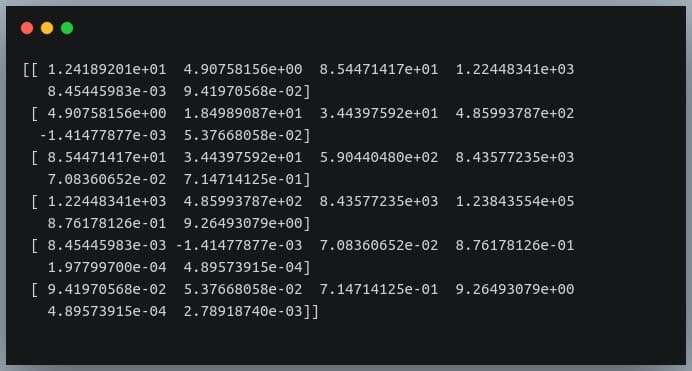
The covariance matrix is a square matrix that summarizes the relationships between multiple variables. Understanding how to interpret this matrix is crucial for gleaning insights about how variables change together. The diagonal elements of the covariance matrix represent the variance of each individual variable. A higher value indicates greater variability in that variable. The off-diagonal elements reveal the covariance between pairs of variables. This number reflects the degree to which two variables change in tandem. Calculating the covariance of a matrix python becomes essential to reveal hidden patterns of data changing together.
A positive covariance indicates that as one variable increases, the other tends to increase as well. Conversely, as one decreases, the other tends to decrease. A negative covariance suggests an inverse relationship. As one variable increases, the other tends to decrease, and vice-versa. It’s important to understand that the magnitude of the covariance alone doesn’t tell the whole story. A large covariance does not necessarily mean a strong relationship. The scale of the variables influences the covariance value. Therefore, comparing covariances across different datasets or different pairs of variables within the same dataset can be misleading if the variables have different units or scales. Calculating the covariance of a matrix python needs careful handling of data scales.
While covariance reveals the direction of the relationship (positive or negative), it doesn’t provide a standardized measure of strength. For instance, a covariance of 10 between two variables measured in meters might seem significant. However, a covariance of 10 between two variables measured in kilometers would indicate a much weaker relationship. To address this limitation, correlation is often used. Correlation standardizes the covariance by dividing it by the product of the standard deviations of the variables. This results in a value between -1 and 1, making it easier to compare the strength of relationships across different datasets. The covariance of a matrix python provides a foundation for further analysis using correlation, which offers a more interpretable measure of association. Remember, interpreting the covariance matrix requires careful consideration of the context and scale of the variables involved. Keep in mind that covariance and correlation only describe linear relationships and might not capture more complex, non-linear associations between variables.
Pythonic Alternatives: Leveraging Pandas for Calculating Data Dispersion
Pandas stands out as a robust Python library, adept at data manipulation and analysis. It offers a streamlined approach to calculating the covariance of a matrix python. Leveraging Pandas simplifies the process, providing intuitive methods for determining the covariance matrix of datasets. Pandas excels in handling labeled data, ensuring accurate alignment during covariance calculations. This eliminates potential errors stemming from misaligned data points. The library’s DataFrame structure organizes data into rows and columns, mirroring the structure of spreadsheets or SQL tables. This familiar format facilitates data exploration and manipulation. Pandas’ automatic data alignment feature is particularly beneficial when working with datasets containing different indices or labels.
To calculate the covariance of a matrix python using Pandas, one can employ the `.cov()` method directly on a DataFrame object. First, one must import the Pandas library. Then, create a DataFrame from your dataset. Following this, calling the `.cov()` method on the DataFrame computes the covariance matrix. The resulting matrix reveals the relationships between different columns (variables) within the DataFrame. The code below exemplifies this process:
Beyond the Basics: Advanced Techniques for Handling Data Dispersion
When working with real-world datasets, calculating the covariance of a matrix python often involves addressing complexities like missing values and the need to weight observations differently. These situations require advanced techniques to ensure accurate and reliable results. NumPy and Pandas provide tools to handle these challenges effectively. Understanding how to use these tools is crucial for robust data analysis.
Missing data can significantly impact covariance calculations. A straightforward approach is to use NumPy’s masked array functionality. The `numpy.ma.cov` function can compute the covariance matrix while ignoring masked (missing) values. For example, if a dataset has missing entries represented as `NaN`, you can create a masked array and then calculate the covariance. This ensures that the missing values do not distort the results. Pandas also offers ways to handle missing data when calculating covariance; the `.cov()` method, by default, excludes missing values pairwise. This means that for each pair of columns, only rows with non-missing values in both columns are considered. The covariance of a matrix python calculated this way will be more accurate than simply imputing the missing values with an arbitrary number. Furthermore, you might need to assign different weights to different observations. This is particularly relevant when some data points are considered more reliable or representative than others. While NumPy’s `cov()` function doesn’t directly support weights, `numpy.ma.cov` can accept weights when dealing with masked arrays. Pandas, again, does not natively support weighting observations directly within the `.cov()` method. For weighted covariance calculations in Pandas, you would need to implement a custom weighting scheme using NumPy and apply it to the data before calculating covariance. In specific scenarios with outliers, consider robust covariance estimators, though these are typically found in more specialized statistical packages.
Consider this python example using `numpy.ma.cov` to handle missing data and weights when computing the covariance of a matrix python:
Limitations of Data Dispersion: When to Be Cautious
Covariance, while valuable, possesses limitations as a sole measure of association. A primary concern is its sensitivity to the scale of the variables. This sensitivity makes direct comparisons of the strength of relationships between different variable pairs challenging. For instance, a covariance of 10 between two variables measured in meters might seem substantial, but it could be insignificant if the variables were measured in millimeters. A solution to this scaling problem lies in using correlation.
Correlation serves as a normalized measure of association, effectively addressing the scale-dependency issue inherent in covariance. Correlation coefficients, ranging from -1 to +1, provide a standardized way to assess the strength and direction of linear relationships. A correlation close to +1 indicates a strong positive relationship, a value near -1 suggests a strong negative relationship, and a value around 0 implies a weak or no linear relationship. When calculating the covariance of a matrix python, it’s important to recognize that high covariance does not automatically imply a strong or meaningful relationship; the scales of the variables must be considered. Therefore, while determining the covariance of a matrix python, remember to consider the scale.
Another critical consideration is the potential for spurious relationships. Covariance or correlation might suggest an association between two variables when, in reality, the relationship is driven by a confounding variable. For example, ice cream sales and crime rates might show a positive covariance; however, this doesn’t mean that ice cream consumption causes crime. A confounding variable, such as warmer weather, likely influences both. Furthermore, it’s crucial to differentiate between correlation and causation. Correlation indicates an association, but it does not prove that one variable causes the other. Establishing causation requires rigorous experimental design and control of confounding variables. When exploring the covariance of a matrix python, researchers and data scientists should always remain aware of the potential for misleading interpretations and strive to identify and account for potential confounding factors to draw accurate and meaningful conclusions.
Data Dispersion in Action: Real-World Application Examples
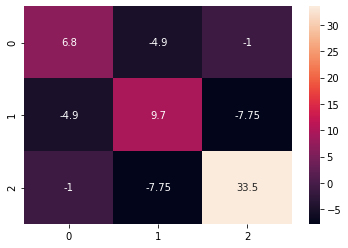
Covariance plays a vital role across various disciplines, offering insights into the relationships between variables. In finance, understanding the covariance of a matrix python is crucial for portfolio optimization. Financial analysts use the covariance of a matrix python to assess how different assets move in relation to each other. By calculating the covariance between asset returns, they can construct portfolios that minimize risk for a given level of return, or maximize return for a given level of risk. A positive covariance indicates that two assets tend to move in the same direction, while a negative covariance suggests they move in opposite directions. This information is used to diversify portfolios and reduce overall volatility. Visualizing the covariance of a matrix python through heatmaps offers a clear understanding of assets’ relationships.
Image processing also leverages the covariance of a matrix python for feature extraction. In image analysis, calculating the covariance between pixel intensities in different regions of an image can help identify patterns and textures. For instance, the covariance matrix of pixel values in a specific area can be used to extract features that describe the texture of that region. These features can then be used for tasks such as image classification and object detection. Understanding the covariance of a matrix python in image processing allows algorithms to differentiate between different textures or patterns within images. These techniques are vital in fields such as medical imaging, remote sensing, and computer vision, where identifying subtle variations in image data is crucial.
In machine learning, the covariance of a matrix python is fundamental to Principal Component Analysis (PCA). PCA is a dimensionality reduction technique that transforms a dataset into a new set of uncorrelated variables called principal components. The first step in PCA involves calculating the covariance matrix of the original data. The eigenvectors of the covariance matrix represent the principal components, and the eigenvalues represent the amount of variance explained by each component. By selecting the top few principal components, we can reduce the dimensionality of the data while retaining most of its variance. This is beneficial for simplifying models, reducing computational cost, and improving model performance. Furthermore, visualizing the covariance matrix via tools like `matplotlib` and `seaborn` aids in comprehending the relationships within the dataset, making PCA’s application more effective. The ability to compute and interpret the covariance of a matrix python is therefore an essential skill for data scientists and machine learning engineers. Visual representations, like heatmaps generated by `matplotlib` and `seaborn`, make these complex relationships more accessible and actionable.
Best Practices: Ensuring Accuracy and Efficiency in Data Dispersion Calculation
When calculating and interpreting the covariance of a matrix python, several best practices should be observed to ensure accuracy and derive meaningful insights. First, data cleaning is paramount. Address missing values appropriately, either by imputation techniques or removal, depending on the extent and nature of the missing data. Inconsistent data should be identified and corrected or removed to prevent skewing the results. Choosing between NumPy and Pandas for calculating the covariance of a matrix python depends on the specific requirements of the task. NumPy is ideal for numerical computation with arrays, while Pandas offers additional functionalities for data manipulation, labeled data handling, and automatic data alignment, streamlining the process of covariance calculation in a DataFrame.
Be mindful of the limitations of covariance as a measure of association. Covariance is sensitive to the scale of the variables, making it difficult to compare relationships between different pairs of variables directly. Consider using correlation as a normalized measure to overcome this limitation. When dealing with missing data in NumPy, leverage `numpy.ma.cov` for handling masked arrays. For weighted observations, ensure the weights are appropriately normalized. Explore robust covariance estimators if outliers are a concern. Always test your code thoroughly with sample datasets to validate the covariance of a matrix python results. Compare the calculated covariance matrix with expected values or results from alternative software packages to ensure the implementation is correct. This includes checking for symmetry (the covariance matrix should be symmetric) and positive semi-definiteness.
Furthermore, the interpretation of the covariance of a matrix python should always be done with caution, considering potential spurious relationships and confounding variables. Remember that correlation does not imply causation, and further investigation may be needed to establish causal relationships. Visualizing the covariance matrix using heatmaps generated with libraries like `matplotlib` or `seaborn` can improve interpretability, particularly for high-dimensional datasets. These visualizations can help identify patterns and relationships between variables more easily. Adhering to these best practices will enhance the reliability and validity of data dispersion analysis using covariance of a matrix python, enabling more informed decision-making based on the insights gained.