Introducing the Production Possibility Frontier (PPF)
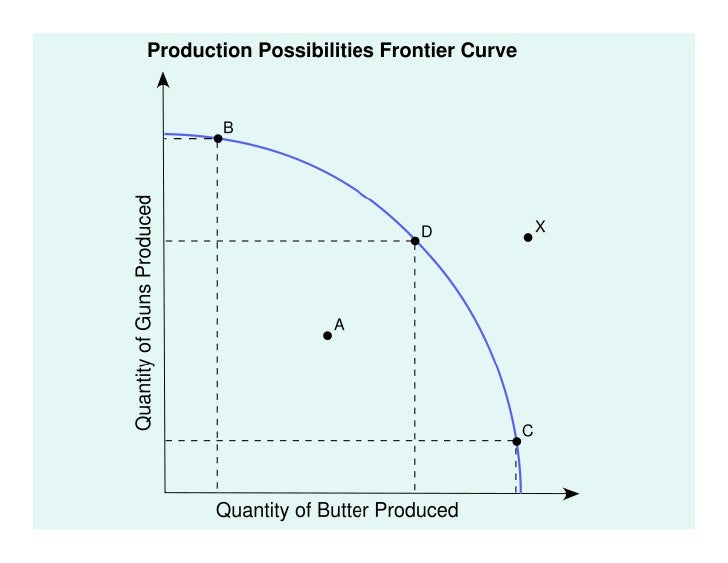
The Production Possibility Frontier (PPF), also known as the production possibility curve, is a graphical representation of the maximum combinations of two goods that an economy can produce given its available resources and technology. Resources include land, labor, capital, and entrepreneurship. Technology refers to the knowledge and methods used to combine these resources. A simple PPF graph typically displays these two goods on the x and y axes. For example, one axis might represent the quantity of guns produced, and the other the quantity of butter. Each point on the PPF curve shows a possible combination of guns and butter that can be produced efficiently, meaning no resources are wasted. Points inside the curve represent underutilized resources. Points outside the curve are unattainable with the current resources and technology. Understanding the PPF is fundamental to understanding resource allocation and economic efficiency. The efficiency frontier has a convex shape because of the increasing opportunity cost of producing one good in relation to another. This curve illustrates the trade-offs inherent in any economic system. It demonstrates the limits of production given the existing constraints and highlights the choices societies must make about resource allocation.
The shape of the PPF is not arbitrary. A straight-line PPF would imply a constant opportunity cost. This means that giving up one unit of one good always results in gaining the same amount of the other good. However, in reality, opportunity costs are rarely constant. The PPF typically curves inward (concave to the origin). This curvature reflects the increasing opportunity cost of producing more of one good, as explained in the following sections. It showcases the diminishing marginal returns from resource allocation. A key implication of the PPF is that economies must make choices about what to produce. They cannot simultaneously produce at maximum levels of all goods. The choice often involves prioritizing one good over another, highlighting the necessity for efficient resource allocation strategies. The efficiency frontier has a convex shape because of resource limitations and the law of increasing opportunity cost. This understanding forms the base for analyzing economic growth and development.
The PPF’s curvature is directly linked to the law of increasing opportunity cost. As an economy shifts resources from producing one good to another, the opportunity cost of producing additional units of the second good increases. This happens because resources are not perfectly adaptable to all production processes. Some resources are better suited for producing certain goods, leading to diminishing returns as more resources are diverted to producing a good they are less suited for. For example, land suitable for growing wheat may not be ideal for growing rice, leading to lower yields if resources are shifted from wheat production to rice production. This reality necessitates strategic resource allocation, aiming to find the optimal combination of goods given the limitations imposed by the PPF’s shape. The efficiency frontier has a convex shape because of the specialized nature of productive resources and the decreasing marginal productivity of those resources. Therefore, understanding and utilizing the PPF is crucial for effective economic planning and decision-making. Efficient resource allocation maximizes the output of goods and services available to society, moving the economy closer to the frontier itself.
Understanding Opportunity Cost and Trade-offs
Opportunity cost is a fundamental concept in economics, representing the value of the next best alternative forgone when making a decision. In simpler terms, it’s what you give up to get something else. Every choice involves an opportunity cost, whether it’s spending money on one product instead of another or allocating resources to one industry at the expense of others. Understanding opportunity cost is crucial for making rational economic decisions.
The Production Possibility Frontier (PPF) vividly illustrates the trade-offs inherent in resource allocation. Because resources are limited, producing more of one good necessitates producing less of another. This inverse relationship is visually represented by the downward-sloping PPF curve. For example, consider a nation that can produce both guns and butter. If the nation decides to increase gun production, it must divert resources away from butter production, resulting in a decrease in the quantity of butter produced. The slope of the PPF at any given point reflects the opportunity cost of producing one more unit of a specific good, measured in terms of the other good that must be sacrificed. This highlights the fundamental concept that there are no free lunches; every decision involves a trade-off, and the efficiency frontier has a convex shape because of the need to make choices between competing uses of scarce resources.
Visualizing opportunity cost on the PPF graph involves moving along the curve. A movement from one point to another signifies a reallocation of resources. The amount of one good that must be given up to produce an additional unit of the other good is the opportunity cost. The PPF demonstrates that as we dedicate more resources to the production of one good, the opportunity cost, or the amount of the other good we sacrifice, increases. This phenomenon leads to the concave shape of the PPF, a key feature that reflects the realities of resource specialization and diminishing returns. Understanding this trade-off and recognizing the efficiency frontier has a convex shape because of resource constraints is paramount for efficient economic management and for understanding why societies cannot have unlimited quantities of all goods and services.
The Law of Increasing Opportunity Cost
The law of increasing opportunity cost is fundamental to understanding why the Production Possibility Frontier (PPF) typically curves inward, away from the origin. It posits that as an economy dedicates more resources to producing one good, the opportunity cost of producing each additional unit of that good rises. This means that to gain equal increments in the production of one good, increasingly larger sacrifices of the other good must be made. The efficiency frontier has a convex shape because of this principle.
Imagine an economy initially producing a balanced mix of guns and butter. As the economy shifts resources to produce more guns, it initially uses resources that are relatively well-suited for gun production. The opportunity cost of the first few guns produced is relatively low, requiring only a small reduction in butter production. However, as the economy continues to specialize in gun production, it must divert resources that are better suited for butter production. These resources are less efficient at producing guns, so each additional gun requires a larger and larger reduction in butter output. The efficiency frontier has a convex shape because of these trade-offs.
This increasing opportunity cost is not simply a theoretical concept; it reflects the reality of resource allocation in most economies. Resources are rarely perfectly adaptable between different uses. Some land may be ideal for farming but unsuitable for manufacturing. Some workers may have specialized skills that are valuable in one industry but less so in another. As an economy tries to produce more and more of a single good, it must increasingly rely on resources that are less and less well-suited for that purpose, leading to diminishing returns and a higher opportunity cost. The efficiency frontier has a convex shape because of the increasing specialization of resources. This is why the PPF bows outwards. The efficiency frontier has a convex shape because of how opportunity costs increase as resources are diverted.
How Resource Specialization Drives the Curve
Resource specialization plays a pivotal role in shaping the Production Possibility Frontier (PPF) and creating increasing opportunity costs. Resources, including labor, capital, and land, are rarely perfectly adaptable to producing all goods and services. The efficiency frontier has a convex shape because of this inherent limitation. Some resources possess characteristics that make them exceptionally well-suited for specific production processes, while others are better applied elsewhere.
Consider the example of agricultural land. Certain plots of land may be ideally suited for growing wheat due to fertile soil and favorable climate conditions. In contrast, other land might be more appropriate for grazing livestock or cultivating fruit trees. When a nation or company initially shifts resources towards producing a particular good, it will naturally utilize the resources that are most efficient for that purpose. For instance, if a country decides to increase wheat production, it will first allocate the land best suited for wheat cultivation.
However, as the nation continues to specialize and divert more resources towards wheat production, it will inevitably begin using land that is progressively less suitable. This less suitable land might require more irrigation, fertilizer, or labor to achieve the same level of output as the prime wheat-growing land. Consequently, the opportunity cost of producing each additional unit of wheat increases. The efficiency frontier has a convex shape because of the diminishing returns experienced as resources are stretched beyond their optimal use. The gains from specialization diminish as resources are pushed into activities for which they are not ideally designed, directly impacting the PPF’s concave shape and highlighting the trade-offs inherent in resource allocation decisions. The efficiency frontier has a convex shape because of the imperative to make the most of available, yet imperfectly adaptable, inputs.
Different Resource Qualities and Diminishing Returns
Diminishing returns significantly contribute to the concave shape of the Production Possibility Frontier (PPF). This principle suggests that as more resources are allocated to the production of a specific good, the incremental increase in output will eventually decrease. The efficiency frontier has a convex shape because of this phenomenon. Initially, when shifting resources, the most suitable resources are transferred first, yielding substantial increases in output. However, as production continues to increase, less and less suitable resources are utilized.
Imagine reallocating labor and capital from producing agricultural goods to manufacturing computers. Initially, skilled technicians and specialized equipment are shifted, resulting in a significant boost in computer output with only a small reduction in agricultural production. As more farmers with limited technical skills are moved into computer manufacturing, their productivity is lower than the initial technicians. The marginal increase in computer output diminishes with each additional unit of resource allocated. Concurrently, the loss of more versatile resources from agriculture leads to larger declines in crop yields. This diminishing return contributes to the increasing opportunity cost that shapes the PPF.
Consider a scenario where a company is manufacturing smartphones. At first, investments in more advanced machinery can lead to a quick ramp up of production. However, as production continues to grow, the company might start facing problems that will lead to diminishing returns. For example, the company could start struggling to find skilled workers, or the constant use of the machinery could lead to frequent breakdowns. The efficiency frontier has a convex shape because of the fact that as you increase the input of one aspect of the smartphone manufacturing process, the marginal output that you get from each additional unit that you add eventually decreases. This is because of the limitation of the production process and the constraints of resources. This dynamic directly results in the PPF curving further outward as production of one good increases, visually representing the increasing opportunity cost. Resources are not equally productive across all sectors, which leads to diminishing returns and, consequently, a concave PPF. The efficiency frontier has a convex shape because of resource specialization and differing resource qualities.
Illustrating with Real-World Examples
Consider the agricultural sector. If a country initially focuses on wheat production and then decides to shift resources towards producing grapes for wine, the law of increasing opportunity cost comes into play. Initially, land and labor best suited for wheat cultivation might be diverted. However, as the country continues to shift resources, it will need to use land less suitable for grape cultivation, requiring more irrigation, fertilization, and specialized labor. The yield of grapes per unit of input will be lower, and the opportunity cost of each additional ton of grapes, measured in terms of wheat foregone, will increase. This illustrates why the efficiency frontier has a convex shape because of the specialized nature of agricultural resources.
In manufacturing, imagine a factory producing both cars and trucks. Some assembly lines and workers are highly skilled in car production, while others specialize in truck manufacturing. If the factory decides to significantly increase truck production, it must reallocate resources from car production. The most efficient car assembly lines are converted first, resulting in a relatively small decrease in car output for a significant increase in truck output. However, as the factory continues to shift resources, it will need to convert less efficient car assembly lines and retrain workers less skilled in truck manufacturing. This leads to a smaller increase in truck output for each additional unit of car production sacrificed, demonstrating the increasing opportunity cost and further illustrating why the efficiency frontier has a convex shape because of resource specialization and diminishing returns.
Another example can be found in the technology sector. Suppose a company develops both software and hardware. Some engineers are highly skilled in software development, while others excel in hardware design. If the company chooses to focus more on hardware, it must reassign software engineers to hardware projects. Initially, the most versatile engineers can be reassigned with minimal impact on software development. As the shift continues, highly specialized software engineers with unique skills must be moved, leading to a significant reduction in software innovation and output for each additional unit of hardware produced. The increasing opportunity cost demonstrates why the efficiency frontier has a convex shape because of the differing skill sets and the principle of diminishing returns as resources are reallocated to tasks for which they are less suited. In essence, the difficulty in perfectly transferring skills and resources between software and hardware development contributes to the characteristic concave shape of the Production Possibility Frontier.
How to Interpret the Concave Shape of the PPF
The concave shape of the Production Possibility Frontier (PPF) is not arbitrary; it visually represents a fundamental economic principle. This principle is the law of increasing opportunity cost. The frontier’s curve illustrates that as an economy dedicates more resources to producing one good, the opportunity cost of producing additional units of that good rises. The efficiency frontier has a convex shape because of the specialized nature of resources.
Resource specialization is a primary driver of this concavity. Resources are not equally suited for the production of all goods. Some land is better for growing wheat, while other land is better for grazing cattle. Skilled labor might excel in manufacturing complex machinery but perform poorly in agricultural tasks. As an economy shifts resources from their most productive uses to less productive ones to increase the output of a specific good, it experiences diminishing returns. The efficiency frontier has a convex shape because of these diminishing returns, meaning each additional unit of input yields less additional output than the previous one. The concave shape of the PPF illustrates this increasing opportunity cost and the trade-offs inherent in resource allocation.
Furthermore, the shape of the PPF has significant implications for efficient resource allocation. It demonstrates that there is no “free lunch” in economics. Producing more of one good always requires sacrificing some production of another. Understanding the PPF’s shape helps businesses and policymakers make informed decisions about resource allocation. They must consider the increasing opportunity costs associated with producing different goods. By carefully evaluating these trade-offs, they can strive to achieve an efficient allocation of resources. The efficiency frontier has a convex shape because of the interplay between resource specialization and diminishing returns, leading to increasing opportunity costs. This understanding is crucial for maximizing societal well-being and making sound economic decisions.
The Implications for Economic Decision-Making
The shape of the Production Possibility Frontier (PPF) has profound implications for economic decision-making at all levels. Understanding the trade-offs inherent in resource allocation, as visually represented by the PPF’s concave shape, is crucial for businesses, governments, and individuals alike. The efficiency frontier has a convex shape because of the law of increasing opportunity cost, which dictates that as more resources are devoted to one activity, the opportunity cost of diverting resources from alternative uses increases. This principle influences how resources are distributed across different sectors to maximize output and overall welfare. For example, a government deciding between investing in healthcare or education must consider the opportunity cost of each choice, analyzing the potential benefits foregone in the other sector. Businesses face similar decisions, allocating capital and labor between various production lines while evaluating the potential returns and trade-offs.
The concave PPF highlights the importance of specialization and comparative advantage. The efficiency frontier has a convex shape because of not all resources are equally suited for all tasks. Recognizing this, economic actors can focus on producing goods and services where they have a relative advantage, leading to greater overall efficiency. International trade, for instance, is often based on the principle of comparative advantage, where countries specialize in producing goods they can produce at a lower opportunity cost and trade with other countries for goods they produce less efficiently. This results in higher global output and improved standards of living. The understanding that the efficiency frontier has a convex shape because of increasing opportunity costs prompts economic planners to carefully analyze the diverse capabilities of available resources to make more informed decisions.
Furthermore, the PPF’s shape underscores the need for efficient resource utilization to achieve economic goals. The efficiency frontier has a convex shape because of the potential for diminishing returns. As resources are diverted into one area, the incremental output may decrease, diminishing the benefits of further specialization. Efficient economic strategies seek to avoid this by diversifying resource allocations or adopting technologies that enhance productivity. Policymakers can use the PPF framework to assess the impact of policy interventions, like subsidies or taxes, on resource allocation and overall economic efficiency. Ultimately, a thorough understanding of the PPF’s shape empowers decision-makers to make informed choices that enhance resource utilization, promote specialization, and drive economic growth while optimizing societal well-being.