Understanding Interest Rates: The Foundation
Interest rates represent the cost of borrowing money or the return on lending it. When you borrow money, you pay interest; when you lend money, you earn interest. A fundamental distinction exists between the nominal interest rate and the effective interest rate. The nominal interest rate is the stated rate, while the effective interest rate reflects the true cost of borrowing or the actual return on investment after accounting for compounding. For example, a loan with a 5% annual nominal interest rate might result in a higher effective interest rate due to monthly compounding. This difference is crucial when comparing financial products, and understanding the nominal vs effective interest rate is key to making sound financial decisions. Consider a simple savings account: a 6% annual nominal interest rate compounded monthly will yield a slightly higher return than one compounded annually, illustrating the impact of compounding on the effective interest rate. The effective interest rate offers a more accurate representation of the actual cost or return compared to the nominal rate alone. Understanding nominal vs effective interest rate is crucial for navigating various financial situations.
Imagine you deposit $1000 into a savings account with a 5% nominal annual interest rate. If interest is compounded annually, you’ll earn $50 after one year. However, if the interest is compounded monthly, you will earn slightly more than $50 due to the effect of earning interest on interest. This difference, however small it might seem initially, becomes significant over longer periods. This concept is at the heart of understanding the difference between nominal and effective interest rates. The effective interest rate, therefore, provides a more accurate reflection of the true return you receive. Ignoring the impact of compounding on the nominal vs effective interest rate could lead to significant underestimation of the actual return or overestimation of loan costs.
The frequency of compounding significantly impacts the effective interest rate. More frequent compounding—daily, weekly, monthly—leads to a higher effective interest rate than less frequent compounding—quarterly, annually. The nominal interest rate remains the same; however, the effective interest rate increases due to the increased power of compounding. Therefore, when comparing financial products, always consider the nominal vs effective interest rate, not just the stated nominal rate. This will allow you to make informed decisions about borrowing and investing, securing the best possible outcome based on the true cost or return. This difference in nominal vs effective interest rate calculations is often overlooked, leading to miscalculations in both borrowing and investing. A thorough understanding is essential for long-term financial success.
Nominal Interest Rate: The Stated Rate
The nominal interest rate is the stated, or advertised, interest rate on a loan or investment. It represents the percentage of the principal that a lender charges for borrowing money, or that an investor earns on their investment, over a specific period, usually a year. The nominal interest rate doesn’t account for the effects of compounding or other fees. It is simply the face value of the interest rate before any adjustments. Understanding the nuances between nominal vs effective interest rate is key to financial health.
Consider a scenario where a bank offers a personal loan with a nominal interest rate of 6% per year. This means that for every $100 borrowed, the borrower will be charged $6 in interest over the course of one year, before considering any other factors. Similarly, a savings account might advertise a nominal annual interest rate of 2%. This suggests that for every $100 deposited, the account holder will earn $2 in interest by the end of the year, without considering the frequency of interest payments or potential fees. When presented with financial products, such as mortgages, auto loans, or certificates of deposit (CDs), the nominal rate is typically the first piece of information provided. This allows for easy comparison between different offers, but it’s important to dig deeper to understand the true cost or return.
It is vital to distinguish the nominal interest rate from any additional fees or charges associated with the loan or investment. For example, a loan might have a low nominal interest rate but include origination fees, application fees, or other charges that significantly increase the overall cost of borrowing. Similarly, an investment account might have a seemingly attractive nominal interest rate, but also have management fees or other expenses that reduce the actual return. Always look beyond the nominal rate and consider all associated costs to accurately assess the true cost or benefit. To make sound financial decisions, understanding the difference between nominal vs effective interest rate is essential. The nominal rate is a starting point, but the effective interest rate provides a more complete picture of the financial implications.
Effective Interest Rate: The True Cost
The effective interest rate represents the actual annual rate of return on an investment or the true cost of borrowing. This rate considers the impact of compounding interest over a year. It offers a more accurate picture compared to the nominal interest rate. The nominal vs effective interest rate is an important distinction. The nominal rate is simply the stated interest rate, while the effective rate reflects the real return or cost when compounding is factored in.
The frequency of compounding significantly influences the effective interest rate. Compounding can occur monthly, quarterly, daily, or even continuously. The more frequently interest is compounded, the higher the effective interest rate will be. For instance, consider a loan with a nominal interest rate of 5% per year. If the interest is compounded annually, the effective interest rate also remains at 5%. However, if the interest is compounded monthly, the effective interest rate will be slightly higher than 5%. This is because interest earned each month starts earning its own interest in the subsequent months. This highlights the difference between nominal vs effective interest rate.
Understanding the effective interest rate is crucial for making informed financial decisions. When comparing different investment options or loan offers, it’s important to look beyond the nominal rate. Always consider the compounding frequency and calculate the effective interest rate to determine the true cost or return. A seemingly small difference in nominal rates can translate to a substantial difference in effective rates over time, especially for larger amounts or longer durations. The nominal vs effective interest rate discrepancy can have financial implications. Understanding this concept empowers individuals to choose the most beneficial financial products and avoid potential pitfalls.
How to Calculate Effective Interest Rate: A Step-by-Step Guide
Understanding the difference between nominal vs effective interest rate is crucial, but knowing how to calculate the effective interest rate empowers you to make informed financial decisions. The effective interest rate reveals the true cost of borrowing or the real return on investment, considering the power of compounding. Here’s a step-by-step guide to calculating it.
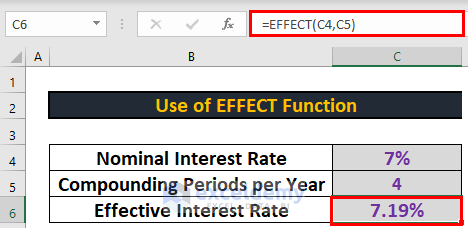
The formula for calculating the effective interest rate is: Effective Interest Rate = (1 + (Nominal Interest Rate / n))^n – 1. Where ‘Nominal Interest Rate’ is the stated annual interest rate, and ‘n’ represents the number of compounding periods per year. For instance, if you have a nominal interest rate of 10% compounded monthly, the calculation would be: Effective Interest Rate = (1 + (0.10 / 12))^12 – 1. First, divide the nominal interest rate (0.10) by the number of compounding periods (12), resulting in approximately 0.00833. Add 1 to this value, giving you 1.00833. Raise this sum to the power of ‘n’ (12), which equals approximately 1.1047. Finally, subtract 1 from this result. Therefore, the effective interest rate is approximately 0.1047, or 10.47%. This illustrates that even with a 10% nominal rate, monthly compounding increases the actual annual interest rate to 10.47%. There are readily available online calculators and spreadsheet functions (like EFFECT in Excel) that can simplify this calculation. Simply input the nominal interest rate and the number of compounding periods, and the calculator will automatically compute the effective interest rate. These tools are especially useful when comparing multiple financial products with varying compounding frequencies. Remember that understanding nominal vs effective interest rate helps you see the true picture.
The variables in the formula play significant roles. A higher nominal interest rate will naturally lead to a higher effective interest rate. However, the number of compounding periods has a multiplying effect. The more frequently interest is compounded, the higher the effective interest rate will be, even if the nominal interest rate remains constant. For example, consider two loans with the same nominal interest rate of 8%. Loan A compounds annually, while Loan B compounds quarterly. Loan A’s effective interest rate will be 8% (since it only compounds once a year). However, Loan B’s effective interest rate will be higher because of the quarterly compounding. Understanding nominal vs effective interest rate, and applying this formula, empowers individuals to make better financial comparisons and decisions, seeing beyond the advertised rate to the true cost or return.
The Impact of Compounding: Understanding the Power of Time
Compounding interest is a powerful concept that significantly impacts the growth of investments and the cost of borrowing. It refers to the process where interest earned in one period is added to the principal, and then the next interest calculation is based on this new, larger principal. This creates a snowball effect, where earnings generate further earnings over time. The more frequently interest is compounded, the faster the principal grows. Understanding compounding is crucial when analyzing the difference between nominal vs effective interest rate. This is because the nominal rate doesn’t account for compounding, while the effective interest rate does.
To illustrate, imagine an initial investment of $1,000 with a nominal interest rate of 10% per year. If the interest is compounded annually, at the end of the first year, the investment will grow to $1,100. In the second year, the 10% interest is calculated on $1,100, resulting in $110 of interest, and a new total of $1,210. However, if the interest is compounded semi-annually (twice a year), the 5% interest is added every 6 months. After the first 6 months, the balance is $1,050. After the next 6 months, the balance grows by 5% of $1,050, or $52.50, resulting in a final balance of $1,102.50. This is higher than the $1,100 earned with annual compounding, even though the nominal vs effective interest rate remains 10%. This small difference highlights the impact of compounding frequency. The more frequent the compounding, the higher the effective interest rate, and the faster the growth. For instance, compounding daily or continuously would yield even greater returns.
Visual aids like charts and graphs can dramatically illustrate the effect of compounding. A simple line graph comparing the growth of an investment with annual compounding versus monthly compounding will visually demonstrate how the investment with more frequent compounding pulls ahead over time. This emphasizes the importance of understanding nominal vs effective interest rate, especially when comparing investments with different compounding frequencies. The difference might seem insignificant in the short term, but over many years or decades, the impact of compounding can be substantial, leading to significantly higher returns. Recognizing this effect is fundamental to sound financial planning and maximizing the benefits of long-term investments.
Nominal vs. Effective Interest Rate: Practical Applications
The distinction between nominal vs effective interest rate significantly impacts real-world financial decisions. Consider comparing loan offers. Bank A offers a loan with a nominal interest rate of 5% compounded annually. Bank B offers a loan with a nominal interest rate of 4.9% compounded monthly. At first glance, Bank B’s offer seems superior. However, the monthly compounding affects the effective interest rate. Calculating the effective interest rate reveals that Bank A’s effective rate remains at 5%, while Bank B’s effective rate is actually closer to 5.01%. Therefore, Bank A’s loan is actually the better deal, despite the higher nominal rate. This highlights the importance of looking beyond the advertised nominal rate.
Another practical application lies in analyzing investment returns. Suppose you are considering two different investment options. Investment X boasts a nominal annual interest rate of 8%, compounded semi-annually. Investment Y offers a nominal annual interest rate of 7.8%, compounded monthly. While Investment X has a higher nominal rate, the more frequent compounding of Investment Y might lead to a higher effective return. Calculating the effective interest rate for both investments will clarify which investment truly yields a better return. Failing to account for the compounding frequency could lead to a suboptimal investment choice. Understanding nominal vs effective interest rate is crucial for maximizing investment gains.
Credit card interest charges also demonstrate the importance of understanding nominal vs effective interest rate. Credit card companies often advertise a nominal annual percentage rate (APR). However, interest is typically calculated and charged on a daily or monthly basis. This compounding effect means the actual cost of carrying a balance on your credit card can be higher than the stated APR suggests. For example, a credit card with a 18% nominal APR, compounded daily, will have a slightly higher effective interest rate than 18%. Therefore, paying off your credit card balance in full each month avoids these compounding interest charges and saves you money. Always consider how compounding affects the true cost of borrowing.
Avoiding Pitfalls: Common Mistakes to Watch Out For
One common mistake is focusing solely on the nominal interest rate. Many borrowers or investors see the advertised rate and fail to consider the compounding frequency. This oversight can lead to significant discrepancies between the expected cost and the actual cost. Understanding the nominal vs effective interest rate difference is crucial to avoid this pitfall. The effective interest rate provides a more accurate representation of the true cost of borrowing or the return on investment, especially over longer periods. Ignoring compounding completely distorts the financial picture. Remember, even seemingly small differences in nominal rates can result in substantial differences in effective rates over time. This is especially true for long-term loans or investments.
Another frequent error is misinterpreting annual percentage rates (APR). While APR aims to provide a standardized measure, it may not always capture all associated fees and charges. Some lenders might include additional fees that inflate the actual cost beyond the stated APR. It’s imperative to thoroughly examine all terms and conditions, including any hidden fees, before committing to a financial product. Always calculate the effective interest rate independently to ensure you have a complete understanding of your financial obligation or return. A comprehensive comparison of different offers requires a clear grasp of nominal vs effective interest rate calculations.
Finally, a lack of understanding of compounding’s impact is a frequent issue. Many individuals underestimate the power of compounding, particularly over extended durations. Compounding interest accelerates the growth of both debt and investments. Therefore, ignoring this aspect leads to inaccurate predictions of future balances. This misunderstanding can cause significant financial repercussions, whether in terms of underestimating loan repayments or overestimating investment earnings. Knowing how to calculate the effective interest rate, considering the compounding frequency, will protect against these errors in evaluating any nominal vs effective interest rate scenario. Accurate financial planning necessitates a full comprehension of these concepts.
Making Informed Financial Decisions: The Bottom Line
In conclusion, understanding the nuances of nominal vs effective interest rate is crucial for navigating the complexities of personal finance. The nominal interest rate, while readily visible, often misrepresents the true cost of borrowing or the actual return on investment. The effective interest rate, however, accounts for compounding, providing a more accurate reflection of the financial implications over time. This difference becomes particularly significant with longer loan terms or investment horizons. A thorough grasp of this distinction empowers consumers to make better decisions regarding loans, investments, and credit cards.
Remember, seemingly small differences in nominal interest rates can translate into substantial variations in effective interest rates. For instance, comparing loan offers solely based on the nominal rate can lead to costly oversights. Similarly, overlooking the compounding frequency when assessing investment returns can significantly underestimate potential gains. Therefore, always prioritize analyzing the effective interest rate before committing to any financial product or service. This proactive approach ensures you are making informed decisions aligned with your financial goals. Financial literacy is key to building a secure financial future.
Ultimately, the knowledge of nominal vs effective interest rate empowers consumers to become more astute financial decision-makers. By focusing on the true cost of borrowing or the actual return on investment, individuals can avoid potential pitfalls and optimize their financial outcomes. This understanding fosters financial independence and contributes to long-term financial well-being. Mastering this concept is a vital step towards responsible financial management.