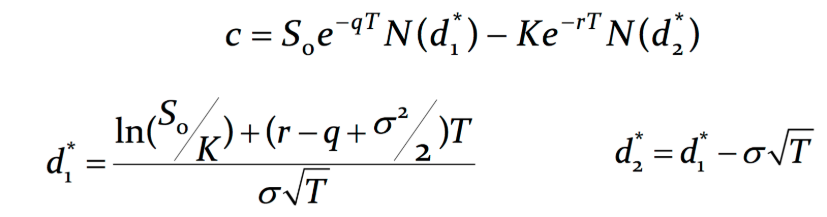Put Call Parity With Dividends

Understanding Put-Call Parity Without Dividends

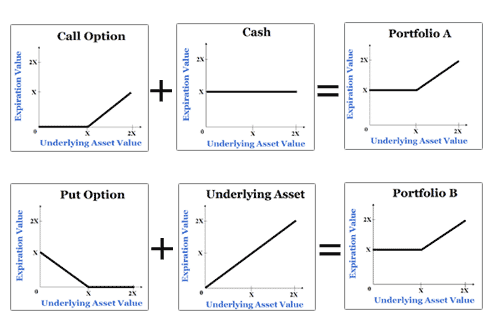
Put-call parity is a fundamental concept in options pricing. It describes a relationship between the price of a European call option and a European put option, both with the same strike price and expiration date, on the same underlying asset. This relationship holds true when no dividends are paid. The theorem essentially states that a portfolio consisting of a long call option and a short put option is equivalent to a portfolio consisting of a long position in the underlying asset financed by borrowing the present value of the strike price. Imagine you have two investment strategies. In one, you buy a call option and simultaneously sell a put option. In the other, you buy the underlying asset and borrow money, promising to repay the strike price at the option’s expiration. These strategies provide identical payoffs regardless of the asset price at expiration. This equivalence highlights the inherent connection between calls and puts and lays the foundation for understanding more complex scenarios such as put call parity with dividends. This equivalence is a result of hedging and risk-neutral pricing principles; sophisticated concepts that are simplified in this fundamental explanation.

The risk-neutral pricing approach assumes that investors are risk-neutral. This means that they don’t demand extra returns for taking on more risk. In a risk-neutral world, the expected return on any investment is simply the risk-free rate of return. Put-call parity holds even under this simplified assumption, because the perfectly offsetting positions in the call and put options effectively eliminate risk. This makes the portfolio’s value predictable and directly linked to the risk-free rate and the underlying asset’s price. The significance of this lies in its implications for arbitrage opportunities; if the prices of the options don’t adhere to the parity relationship, arbitrageurs can profit by exploiting the price discrepancy.

Understanding put-call parity is crucial for option traders and investors. It provides a valuable framework for pricing options and constructing hedging strategies. The core principle of put-call parity forms the base for understanding more advanced scenarios, including the impact of dividends. While the basic theorem illustrates the relationship between calls and puts, introducing dividends adds another layer of complexity, modifying the relationship and creating new opportunities for arbitrage. The understanding of put call parity with dividends is paramount for sophisticated investors and traders aiming to fully grasp option pricing mechanics and potential profits.

How Dividends Affect Options Pricing

Dividends significantly impact put-call parity with dividends. When a company pays a dividend, the underlying stock price typically adjusts downward by roughly the dividend amount. This price decrease affects both call and put options. Call options lose value because the stock price, the asset underlying the option, is lower. This reduces the likelihood of the option finishing in the money. Conversely, put options may see a slight increase in value, as the lower stock price increases the chances of the put option being profitable. Understanding this dynamic is crucial for accurately pricing and using options, especially in the context of put-call parity with dividends.

Consider a simplified example: Imagine a stock trading at $100 before a $1 dividend payment. A call option with a strike price of $105 might be worth $2. After the dividend, the stock price falls to $99. The call option’s value will likely decrease, reflecting the reduced chance of the stock reaching $105. The put option, however, might increase in value because the lower stock price makes it more probable that the stock will fall below the strike price, making the put option profitable. This interplay highlights the importance of factoring dividends into option pricing models, including the adjustments required for put-call parity with dividends. Visualizing these changes with a graph showing the stock price and option values before and after the dividend would further clarify the impact.

The effect of dividends on put-call parity is not merely a minor adjustment. It’s a fundamental change that alters the relationship between call and put prices. Ignoring dividends leads to mispriced options and potential arbitrage opportunities. Therefore, accurately applying put-call parity with dividends requires a precise understanding of the dividend’s impact on both the underlying asset and the options written on that asset. This ensures accurate valuation and the development of sound hedging strategies. The precise mechanics are detailed in the adjusted put-call parity formula, further clarifying the relationship between options prices and dividend payments in the context of put-call parity with dividends.

The Modified Put-Call Parity Formula with Dividends

The standard put-call parity theorem requires adjustment to account for dividend payments. Dividends impact option pricing because the underlying asset’s price typically falls by roughly the dividend amount on the ex-dividend date. This decrease affects the potential payoff of both call and put options. The modified formula incorporates the present value of future dividends to accurately reflect this impact on put-call parity with dividends. The adjusted formula is: C + PV(Div) = P + S, where:

C represents the price of a European call option. P represents the price of a European put option. S represents the current price of the underlying asset. PV(Div) signifies the present value of all dividends expected to be paid before the options expire. This calculation discounts future dividend payments back to the present using the risk-free interest rate. The formula demonstrates that the relationship between call and put options remains, but the present value of dividends must be added to the call option price to maintain parity. Understanding put-call parity with dividends is crucial for accurate option valuation and arbitrage identification. The derivation of this modified formula involves considering the replicated portfolio strategy in a dividend-paying environment. The portfolio that replicates the payoff of a call option, in the case of dividend-paying assets, includes the present value of the dividend payments received. This modification ensures that the risk-neutral pricing approach remains consistent, even when dividends are factored into the equation.

Calculating the present value of dividends is key to applying the put-call parity with dividends formula effectively. The present value (PV) is determined by discounting each future dividend payment back to its present value using the risk-free interest rate and the time until the dividend is paid. For instance, if a stock is expected to pay a dividend of $1 in three months, and the risk-free interest rate is 5% per annum, the present value of this dividend would be approximately $0.9876 ($1 / (1 + 0.05/4)). This calculation is then repeated for each dividend payment before the option expiration date, and all the present values are summed to obtain the total PV(Div). This sum is then incorporated into the put-call parity with dividends equation. By accurately estimating the present value of dividends, one gains a better understanding of the fair price relationships between options and the underlying assets, enhancing investment decisions related to put-call parity with dividends.

Practical Applications of Put-Call Parity with Dividends

Understanding put call parity with dividends extends beyond theoretical exercises and finds significant application in real-world financial scenarios. Its understanding is crucial for informed decision-making, particularly in markets involving dividend-paying stocks. One primary application is in identifying potential arbitrage opportunities, where deviations from the parity relationship can be exploited to generate risk-free profits. These opportunities arise when market prices of call options, put options, the underlying stock, and the present value of expected dividends do not align with the put call parity with dividends formula. Skilled traders can capitalize on these discrepancies by simultaneously buying and selling the mispriced assets, locking in a profit with minimal risk.

Furthermore, put call parity with dividends plays a vital role in constructing effective hedging strategies. Investors holding dividend-paying stocks can use options in conjunction with the underlying asset to mitigate potential losses from price fluctuations and dividend payouts. For example, a protective put strategy, combined with an understanding of how dividends affect option prices, allows investors to protect their downside risk while still benefiting from potential upside gains. Similarly, covered call strategies can be refined by considering the impact of dividends on the call option’s premium. The put call parity with dividends relationship enables investors to precisely calculate the appropriate hedge ratios and adjust their positions to maintain a desired level of risk exposure. This is particularly important for institutional investors managing large portfolios of dividend-paying equities.

Option valuation on dividend-paying assets is another area where put call parity with dividends proves invaluable. While models like Black-Scholes are widely used, they often require adjustments to account for dividends. Put call parity provides an alternative method for estimating the fair value of an option, particularly when market data for one of the options (either the call or the put) is readily available. By knowing the price of the underlying asset, the dividend yield, and the price of the other option, the theoretical price of the less liquid option can be derived using the adjusted put call parity formula. This is helpful for traders and analysts in assessing whether an option is overvalued or undervalued in the market. Ultimately, the practical applications of put call parity with dividends are diverse and essential for anyone actively involved in trading or managing investments in dividend-paying stocks. This ensures better informed decisions, minimized risks, and potentially enhanced returns.

Arbitrage Opportunities and Risk-Free Profits

Deviations from put call parity with dividends present potential arbitrage opportunities for astute investors. These opportunities arise when the market prices of the call option, put option, underlying asset, and present value of expected dividends do not align according to the put call parity with dividends relationship. By identifying these mispricings, investors can construct portfolios that generate risk-free profits.

Consider a scenario where the price of a call option is too low relative to the price of the put option, the underlying stock, and the present value of the dividends. Specifically, suppose the put call parity with dividends formula suggests that the call option should be trading at $10, but it is actually trading at $8. An arbitrageur could exploit this discrepancy through the following steps: Simultaneously, the investor buys the undervalued call option for $8 and sells short the put option, the underlying stock, and borrows the present value of the dividends to finance the purchase. This strategy creates a synthetic long call position at a lower cost than its fair value. If, at expiration, the stock price is above the strike price, the call option will be exercised, and the investor will profit from the difference between the stock price and the strike price, less the initial investment. If the stock price is below the strike price, the put option will be exercised, and the investor will be obligated to buy the stock at the strike price. However, this is offset by the short position in the stock, resulting in a net profit. This risk-free profit is secured because the portfolio is designed to be immune to fluctuations in the stock price. The profit comes from the initial mispricing detected by put call parity with dividends.

However, it’s crucial to acknowledge that real-world arbitrage opportunities are often fleeting and small. Transaction costs, such as brokerage commissions and bid-ask spreads, can quickly erode potential profits. Furthermore, the execution of arbitrage trades requires speed and precision, as market prices can adjust rapidly to eliminate mispricings. High-frequency trading firms often employ sophisticated algorithms to identify and exploit these fleeting arbitrage opportunities related to put call parity with dividends, making it challenging for individual investors to consistently profit from such strategies. Despite these challenges, understanding put call parity with dividends remains a valuable tool for investors seeking to identify and capitalize on market inefficiencies.

Using Put-Call Parity for Option Valuation

Put-call parity with dividends serves as a powerful tool for determining the theoretical fair price of either a call or a put option when the price of its counterpart is known, along with the underlying asset’s price and dividend information. This principle stems from the no-arbitrage condition, which dictates that assets with identical payoff profiles must be priced consistently. Any deviation from this parity presents a potential arbitrage opportunity, making its understanding crucial for options traders and investors. The concept of put call parity with dividends allows for a more precise valuation in markets where dividends play a significant role.

To illustrate, consider a scenario involving a stock currently trading at $50. A call option with a strike price of $52.50, expiring in three months, is priced at $3. Simultaneously, the present value of dividends expected to be paid during this period is $1.50. Using the adjusted put-call parity formula (Call Price – Put Price = Stock Price – Strike Price – Present Value of Dividends), one can determine the theoretical price of the corresponding put option. Plugging in the values ($3 – Put Price = $50 – $52.50 – $1.50), simplifies to ($3 – Put Price = -$4). Solving for the Put Price gives a theoretical value of $7. If the put option is trading significantly higher or lower than $7 in the market, it may indicate a potential mispricing relative to the call option and the underlying stock, adjusted for dividends. This application of put call parity with dividends is fundamental for options valuation.

Another example could involve a situation where an investor observes a put option trading at $5, with the stock price at $45 and a call option with the same strike price and expiration trading at $2. Assume the present value of expected dividends before expiration is $0.75. Applying the put call parity with dividends relationship, the formula becomes ($2 – $5 = $45 – Strike Price – $0.75), which simplifies to (-$3 = $44.25 – Strike Price). Solving for the Strike Price, we get $47.25. This implies that the options are priced in accordance with put-call parity if the strike price is indeed $47.25. However, if the strike price differs, it suggests a potential deviation from parity. Therefore, put-call parity with dividends is a cornerstone of options pricing theory and provides a practical framework for investors to evaluate option values and identify potential arbitrage opportunities while considering the impact of dividend payments.

Hedging Strategies Utilizing Put-Call Parity

Put-call parity with dividends is not just a theoretical concept; it’s a powerful tool for constructing sophisticated hedging strategies, particularly for dividend-paying stocks. The core idea is to create a portfolio that is insensitive to price fluctuations in the underlying stock and changes in dividend payouts, effectively neutralizing risk. This is achieved by combining positions in the stock, call options, and put options in a way that exploits the relationship defined by the put-call parity equation. The beauty of this approach lies in its ability to isolate specific risks and manage them effectively.

One common strategy involves creating a synthetic stock position using options. According to put-call parity with dividends, a long call option and a short put option, both with the same strike price and expiration date, are equivalent to holding the underlying stock and receiving the present value of the dividends. An investor can use this relationship to hedge an existing stock holding. For example, if an investor owns shares of a dividend-paying stock and is concerned about a potential price decline before the dividend is paid, they can implement a protective put strategy and simultaneously sell a call option. This strategy profits if the stock price remains stable. The short call position generates income, offsetting the cost of the put option.

Furthermore, dynamic adjustments are crucial for maintaining an effective hedge. As the stock price and time to expiration change, the hedge ratios of the options also change. This means that the investor needs to periodically rebalance the portfolio to maintain the desired risk profile. The dividend yield also plays a key role in the equation, and any changes in expected dividend payouts must be factored into the hedging strategy. By understanding and applying put call parity with dividends, investors can construct robust and adaptable hedging strategies, minimizing their exposure to market volatility and dividend uncertainty. This allows them to manage their portfolios more effectively and achieve their investment goals with greater confidence.

Advanced Considerations and Limitations

While put call parity with dividends provides a valuable framework for understanding options pricing, it’s crucial to acknowledge its limitations and underlying assumptions. The basic put call parity with dividends model operates under idealized conditions that may not perfectly reflect real-world market dynamics. One key assumption is the absence of transaction costs, including brokerage fees and bid-ask spreads. In reality, these costs can erode potential arbitrage profits, making it unprofitable to exploit minor deviations from parity. Similarly, the model assumes efficient markets, where prices instantaneously reflect all available information. However, market inefficiencies can persist, creating temporary mispricings that deviate from put call parity with dividends.

Another important consideration is the assumption of constant interest rates and predictable dividend payments. Fluctuations in interest rates can affect the present value of future dividends, potentially impacting the accuracy of the put call parity with dividends relationship. Furthermore, the model typically assumes that dividends are known and predictable. However, some companies may adjust their dividend policies unexpectedly, introducing uncertainty into the calculation. When dealing with options on index funds, the dividend payouts are often complex and less predictable than those of individual stocks, making the application of put call parity with dividends more challenging. The timing of dividend payments also matters; the parity relationship holds precisely only at the option’s expiration date, requiring adjustments for earlier evaluations. More sophisticated models may incorporate stochastic interest rates and dividend yields to account for these uncertainties and provide a more accurate representation of option pricing.

It’s also worth noting that put call parity with dividends is a theoretical relationship. While it provides a useful benchmark, actual market prices may deviate from the theoretical values due to various factors, including supply and demand imbalances, market sentiment, and liquidity constraints. Understanding these limitations is essential for applying put call parity with dividends effectively and interpreting its implications in real-world trading scenarios. Despite these limitations, put call parity with dividends remains a cornerstone of options theory and provides a valuable tool for understanding the interplay between options, underlying assets, and dividend payments. Sophisticated traders use this framework to identify potential mispricings and construct hedging strategies, always bearing in mind the assumptions and potential deviations from the idealized model.