What is the Null Hypothesis in Simple Linear Regression?
In the realm of simple linear regression, the null hypothesis for linear regression plays a pivotal role. It postulates that there is no relationship between the independent variable (the predictor) and the dependent variable (the outcome). Essentially, it asserts that changes in the independent variable do not lead to predictable changes in the dependent variable.
Mathematically, this translates to the slope of the regression line being equal to zero. If the slope is zero, the regression line is horizontal, indicating that the value of the dependent variable remains constant regardless of the independent variable’s value. The null hypothesis for linear regression serves as a starting point for hypothesis testing, a structured process to determine if there is enough statistical evidence to reject the assumption of no relationship.
The purpose of the null hypothesis for linear regression is to provide a benchmark against which to evaluate the observed data. It allows researchers to determine if the data provides sufficient evidence to conclude that a relationship between the variables truly exists. Hypothesis testing is a cornerstone of statistical inference, allowing researchers to draw conclusions about a population based on a sample of data. In summary, the null hypothesis for linear regression is that the slope of the regression line is zero, indicating no linear relationship between the independent and dependent variables. Its role is to be assessed if we can reject this assumption through statistical tests.
Deciphering the Zero Slope: Interpreting Regression Results
The practical implications of the null hypothesis for linear regression are significant when interpreting regression results. The null hypothesis for linear regression typically states that there is no linear relationship between the independent and dependent variables. This translates to the slope of the regression line being zero. In simpler terms, changes in the predictor variable do not lead to predictable changes in the outcome variable. Understanding this concept is crucial for drawing valid conclusions from statistical analyses.
When conducting a hypothesis test, the p-value plays a vital role. A non-significant p-value, generally above a pre-determined significance level (alpha), suggests that the data does not provide sufficient evidence to reject the null hypothesis for linear regression. This means we fail to find statistically significant evidence of a linear relationship between the variables under investigation. It is essential to understand the nuance here: we do not *accept* the null hypothesis. Instead, we *fail to reject* it. Failing to reject the null hypothesis simply means that, based on the available data, we cannot conclude that a linear relationship exists. There might be a non-linear relationship, the effect might be too small to detect with the current sample size, or there might be no relationship at all. The null hypothesis for linear regression remains a possibility.
It’s crucial to avoid overstating the implications of failing to reject the null hypothesis for linear regression. It does *not* prove that the independent variable has absolutely no effect on the dependent variable. Other factors might be at play. Furthermore, the absence of a statistically significant linear relationship does not preclude the existence of other types of relationships. Therefore, a careful and nuanced interpretation of regression results, considering the limitations of hypothesis testing, is always necessary. Remember, statistical significance does not always equate to practical significance, and further investigation might be warranted even when the null hypothesis for linear regression cannot be rejected.
How to Perform a Hypothesis Test for Regression Coefficients
A hypothesis test for regression coefficients assesses the statistical significance of the relationship between the independent and dependent variables. In the context of the null hypothesis for linear regression, the null hypothesis typically states that there is no linear relationship. This translates to the slope of the regression line being equal to zero. The alternative hypothesis posits that there is a linear relationship (slope is not zero). The hypothesis test helps determine if the observed data provides enough evidence to reject the null hypothesis for linear regression.
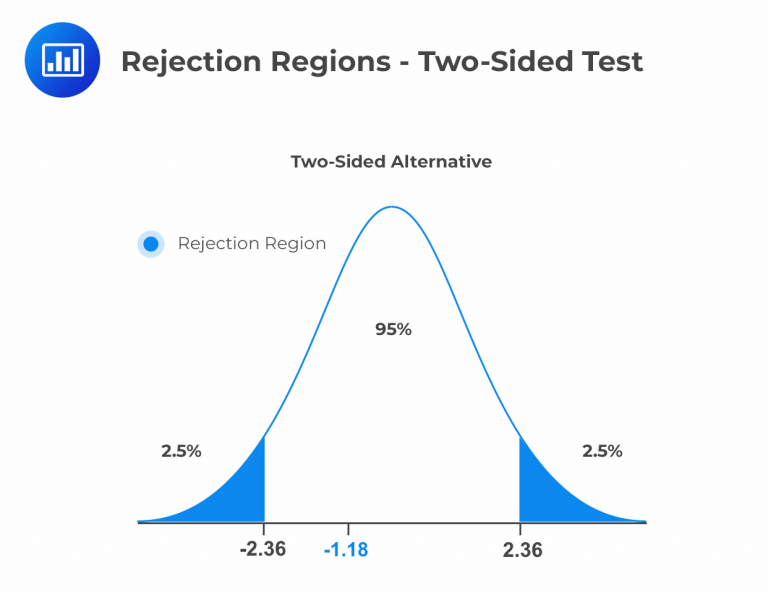
The process involves several key steps. First, define the null hypothesis (H0: β = 0) and the alternative hypothesis (H1: β ≠ 0, for a two-tailed test; or H1: β > 0 or H1: β < 0, for a one-tailed test). Here, β represents the regression coefficient. Next, calculate the test statistic. The most common test statistic is the t-statistic, calculated as (estimated coefficient - hypothesized value) / standard error of the coefficient. Alternatively, an F-statistic can be used, particularly when testing the overall significance of a model with multiple predictors. After computing the test statistic, determine the p-value. The p-value represents the probability of observing a test statistic as extreme as, or more extreme than, the one calculated, assuming the null hypothesis for linear regression is true.
Finally, make a decision based on the chosen significance level (alpha), usually 0.05. If the p-value is less than alpha, we reject the null hypothesis for linear regression. This suggests there is statistically significant evidence of a linear relationship between the variables. Conversely, if the p-value is greater than alpha, we fail to reject the null hypothesis. This indicates that the data does not provide sufficient evidence to conclude a linear relationship exists. Remember to consider whether a one-tailed or two-tailed test is appropriate based on the research question. A two-tailed test examines if the coefficient is simply different from zero, while a one-tailed test examines if it is either greater than or less than zero.
Factors Influencing Hypothesis Testing Outcomes in Linear Models
Several factors can influence the outcome of a hypothesis test in linear regression, affecting the ability to accurately assess the null hypothesis for linear regression. These factors impact the power of the test, which is the probability of correctly rejecting the null hypothesis when it is false. Understanding these influences is crucial for interpreting regression results.
Sample size is a primary factor. Larger samples provide more information, increasing the test’s power. With a larger sample, even small deviations from the null hypothesis for linear regression (i.e., a slope of zero) may become statistically significant. Conversely, small samples may lack the power to detect a real relationship, leading to a failure to reject the null hypothesis even when it is false. Variability in the data also plays a significant role. Greater variability, or noise, in either the independent or dependent variable makes it harder to detect a true underlying relationship. This increased variance reduces the test’s power. The strength of the relationship between the variables is another key determinant. A strong linear relationship is easier to detect than a weak one. The weaker the actual relationship, the larger the sample size needed to reject the null hypothesis for linear regression.
Outliers can exert a disproportionate influence on regression results. A single outlier can dramatically alter the estimated regression coefficients and inflate the error variance, potentially leading to either a false rejection or a failure to reject the null hypothesis for linear regression. It is essential to identify and address outliers appropriately, either by removing them (if justified) or by using robust regression techniques that are less sensitive to extreme values. The choice of significance level (alpha) also directly affects the outcome. A smaller alpha (e.g., 0.01 instead of 0.05) makes it harder to reject the null hypothesis, reducing the risk of a Type I error (false positive) but increasing the risk of a Type II error (false negative). Careful consideration of these factors is essential for drawing valid conclusions from hypothesis tests in linear regression and properly testing the null hypothesis for linear regression.
Relationship Between P-values and Hypothesis Testing
Understanding p-values is crucial for interpreting the results of a null hypothesis for linear regression. The p-value represents the probability of obtaining results as extreme as, or more extreme than, the observed results, assuming the null hypothesis is true. In simpler terms, it quantifies the evidence against the null hypothesis. A smaller p-value indicates stronger evidence against the null hypothesis. This evidence relates directly to the null hypothesis for linear regression; a small p-value suggests a statistically significant relationship between the variables, while a larger p-value suggests the opposite.
To conduct a hypothesis test for the null hypothesis for linear regression, the p-value is compared to a pre-determined significance level, often denoted as alpha (α). This significance level represents the probability of rejecting the null hypothesis when it is actually true (Type I error). A commonly used significance level is 0.05. If the p-value is less than α, the null hypothesis is rejected. This means there is sufficient evidence to suggest a statistically significant relationship. Conversely, if the p-value is greater than or equal to α, the null hypothesis is not rejected; there is insufficient evidence to conclude a relationship exists. It is important to remember that failing to reject the null hypothesis does not prove it is true. It simply means the data do not provide enough evidence to reject it.
It’s critical to emphasize that the p-value is not the probability that the null hypothesis is true. This is a common misconception. The p-value only reflects the probability of the observed data (or more extreme data) given that the null hypothesis is true. Therefore, a high p-value does not mean the null hypothesis is likely true; it only indicates a lack of evidence to reject it. Proper interpretation of p-values within the context of the null hypothesis for linear regression is essential for drawing valid conclusions from regression analyses. Misinterpreting p-values can lead to flawed conclusions about the relationships between variables. Always consider the practical significance of your findings in addition to the statistical significance indicated by the p-value.
Common Mistakes in Interpreting Hypothesis Tests for Regression
Interpreting hypothesis tests for regression, particularly the null hypothesis for linear regression, requires careful consideration. A common pitfall is confusing statistical significance with practical significance. A statistically significant result (rejecting the null hypothesis) simply indicates that the observed relationship is unlikely due to chance alone. However, this doesn’t necessarily mean the relationship is practically important or meaningful. A small effect size, even if statistically significant, may not have real-world implications. Conversely, a large effect size might not achieve statistical significance due to small sample size or high variability. Always consider the magnitude of the effect and its context alongside the p-value when evaluating the findings. The null hypothesis for linear regression, when rejected, should always be interpreted cautiously in this light.
Another frequent error is assuming correlation implies causation. Rejecting the null hypothesis for linear regression only demonstrates an association between variables. It doesn’t prove that one variable causes changes in the other. Confounding variables or spurious correlations can lead to incorrect causal inferences. Therefore, it is crucial to consider alternative explanations and conduct further research to establish causality. Remember, even a strong correlation, as shown by a rejected null hypothesis for linear regression, doesn’t automatically imply a causal link. Always consider potential confounding factors and use appropriate research designs to understand the nature of the relationships between variables.
Finally, limitations of hypothesis testing in regression should be recognized. Hypothesis testing is based on probabilities; it does not provide definitive proof. A failure to reject the null hypothesis doesn’t confirm the absence of a relationship; it simply means that the data doesn’t provide enough evidence to reject the null hypothesis for linear regression at the chosen significance level. Similarly, rejecting the null hypothesis does not guarantee a strong or reliable relationship. Factors like sample size and data variability influence the test’s power, meaning a low-powered test might fail to detect a real relationship, while a high-powered test might exaggerate the significance of a weak one. Consider these limitations when interpreting the results of your hypothesis test for the null hypothesis for linear regression, always bearing in mind that careful consideration and further investigation are always necessary.
Beyond Simple Linear Regression: Extensions to Multiple Regression
The concept of the null hypothesis extends seamlessly to multiple linear regression. In this more complex scenario, multiple independent variables predict a single dependent variable. The null hypothesis for linear regression is adapted to test the significance of each individual predictor variable. For each predictor, the null hypothesis states that its coefficient is equal to zero, holding all other variables constant. This means there’s no relationship between that specific predictor and the outcome variable, given the presence of other predictors in the model. Failing to reject this null hypothesis indicates that the independent variable does not significantly contribute to explaining the variance in the dependent variable, considering the effects of other variables.
Unlike simple linear regression which often uses t-tests, multiple regression frequently employs F-tests to assess the overall model significance. The F-test evaluates the null hypothesis that all regression coefficients are simultaneously equal to zero. Rejecting this null hypothesis suggests that at least one predictor variable significantly contributes to explaining the variation in the dependent variable. This is a crucial overall assessment of model fit and predictive power, before examining the individual predictor significance. Understanding both the individual and overall tests is key to interpreting a multiple linear regression model effectively. The null hypothesis for linear regression remains central in determining the significance of the model and its individual predictors.
The interpretation of p-values remains critical. A low p-value for an individual predictor, following the principles of the null hypothesis for linear regression, suggests strong evidence against the null hypothesis and supports the conclusion that the predictor is significantly associated with the dependent variable. Similarly, a low p-value for the overall F-test suggests the model as a whole is statistically significant. It is vital to remember that even with significant results, correlation does not equal causation. Careful consideration of potential confounding variables and the context of the study are crucial for accurate interpretation of the results. Thorough analysis helps you understand the relationships revealed by testing the null hypothesis for linear regression.
Assessing Model Validity After Hypothesis Testing in Regression Analysis
After conducting hypothesis tests for the null hypothesis for linear regression, it’s crucial to evaluate the regression model’s validity. This involves checking several key assumptions. Violation of these assumptions can lead to inaccurate or misleading inferences about the relationship between variables. A robust model requires careful attention to these details. The most important assumptions to verify are linearity, independence of errors, homoscedasticity, and normality of residuals.
Linearity assumes a linear relationship between the independent and dependent variables. If this assumption is violated, the results of the null hypothesis for linear regression test might be unreliable. Techniques like residual plots can visually assess linearity. Transformations of variables (e.g., logarithmic transformations) can sometimes address non-linearity. Independence of errors means that the residuals (the differences between observed and predicted values) are independent of each other. Autocorrelation, where errors are correlated, often violates this assumption. This can occur in time series data. Tests for autocorrelation, such as the Durbin-Watson test, can help detect this issue. Addressing autocorrelation may involve using specialized time series models.
Homoscedasticity, or constant variance of errors, is another critical assumption. Heteroscedasticity, where the variance of errors changes across the range of predictor variables, can lead to inefficient and biased estimates. Residual plots can again reveal heteroscedasticity. Transformations of the dependent variable or weighted least squares regression are possible solutions. Finally, normality of residuals assumes that the residuals are approximately normally distributed. While minor deviations from normality are often acceptable, severe departures can affect the reliability of hypothesis tests, especially with smaller sample sizes. Histograms and Q-Q plots can visually assess normality. Transformations or robust regression techniques can be employed if the assumption is severely violated. Remember, a valid null hypothesis for linear regression relies on the fulfillment of these assumptions. Thorough model diagnostics are essential for ensuring reliable interpretations and drawing accurate conclusions from regression analyses.