What is Expected Utility and Why Does it Matter?
In the realm of decision-making, uncertainty is an inherent aspect that can often lead to indecision. This is where the concept of expected utility comes into play, providing a framework for individuals to make informed choices under uncertain circumstances. Expected utility is a measure of the overall value or usefulness of a particular decision or action, taking into account the probabilities of different outcomes. By learning how to calculate expected utility, individuals can weigh the potential benefits and drawbacks of a decision, ultimately making more confident and informed choices. In essence, understanding expected utility is a crucial skill for anyone looking to improve their decision-making abilities. By grasping this concept, individuals can navigate complex decisions with greater ease, making it an essential tool in various aspects of life, from personal finance to business strategy.
Understanding the Expected Utility Formula: A Step-by-Step Guide
The expected utility formula is a powerful tool for decision-making under uncertainty. It provides a structured approach to evaluating the potential outcomes of a decision, allowing individuals to make informed choices. The formula is expressed as EU = Σ(P × U), where EU represents the expected utility, P denotes the probability of each outcome, and U symbolizes the utility or value associated with each outcome. To calculate expected utility, one must first identify the possible outcomes of a decision and assign a probability to each outcome. Next, the utility or value of each outcome must be determined, which can be done using a utility function. Finally, the probability and utility of each outcome are multiplied together and summed to arrive at the expected utility. By following this step-by-step guide, individuals can learn how to calculate expected utility and make more confident decisions in the face of uncertainty.
How to Calculate Expected Utility: A Real-World Example
Let’s consider a real-world scenario to illustrate how to calculate expected utility. Suppose an investor is deciding between two investment options: a high-risk stock with a potential return of 20% and a low-risk bond with a potential return of 5%. The investor estimates that there is a 60% chance the stock will yield a 20% return and a 40% chance it will result in a 10% loss. On the other hand, the bond is expected to yield a 5% return with 90% certainty. To calculate the expected utility of each investment option, the investor must first assign a utility value to each outcome. For the sake of simplicity, let’s assume the utility values are directly proportional to the returns. Using the expected utility formula, EU = Σ(P × U), the investor can calculate the expected utility of each option. For the stock, EU = (0.6 × 20) + (0.4 × -10) = 8. For the bond, EU = (0.9 × 5) = 4.5. By comparing the expected utilities, the investor can make an informed decision about which investment option to choose. This example demonstrates how to calculate expected utility in a real-world scenario, highlighting the importance of considering both probability and utility when making decisions under uncertainty.
The Role of Probability in Expected Utility Calculations
Probability plays a crucial role in expected utility calculations, as it represents the likelihood of each outcome occurring. When calculating expected utility, it is essential to assign accurate probabilities to each outcome. This can be a challenging task, especially when dealing with uncertain events. To overcome this challenge, individuals can use various techniques to estimate probabilities, such as historical data analysis, expert judgment, or simulation models. It is also important to recognize that probability is a subjective measure, and different individuals may assign different probabilities to the same outcome. Therefore, it is essential to consider multiple perspectives and sources of information when assigning probabilities. Additionally, individuals should be aware of common pitfalls, such as ignoring probability or assigning equal probabilities to all outcomes, which can lead to inaccurate expected utility calculations. By understanding the role of probability in expected utility calculations and how to assign accurate probabilities, individuals can make more informed decisions under uncertainty. For instance, when considering how to calculate expected utility in a real-world scenario, such as investing in stocks, it is essential to estimate the probability of each potential outcome, including the probability of a stock’s value increasing or decreasing. By doing so, individuals can make more informed investment decisions and maximize their expected utility.
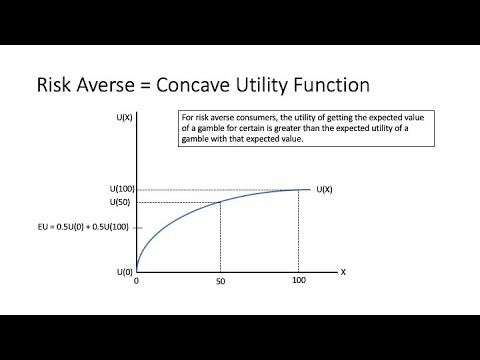
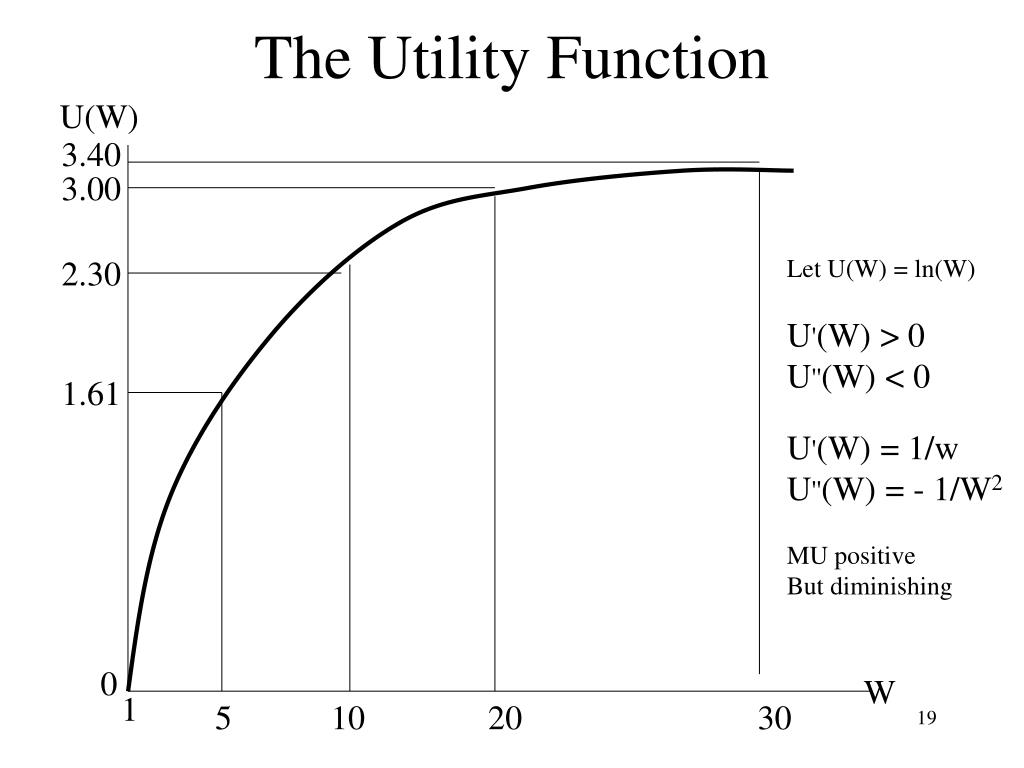
Utility Functions: Measuring Preferences and Values
A utility function is a crucial component in expected utility calculations, as it represents an individual’s preferences and values. In essence, a utility function assigns a numerical value to each possible outcome, reflecting the desirability or undesirability of that outcome. The utility value can be thought of as a measure of the satisfaction or happiness derived from a particular outcome. When constructing a utility function, it is essential to consider the individual’s risk tolerance, preferences, and values. For instance, a risk-averse individual may assign a higher utility value to a certain outcome with a lower return, rather than a risky outcome with a higher potential return. Utility functions can take various forms, including linear, exponential, or logarithmic functions, depending on the individual’s preferences and the nature of the decision. To illustrate, consider a healthcare scenario where a patient must choose between two medical treatments. A utility function can be constructed to reflect the patient’s preferences for different health outcomes, such as the probability of recovery, quality of life, or potential side effects. By using a utility function, the patient can calculate the expected utility of each treatment option and make an informed decision. Understanding how to construct a utility function is vital in expected utility calculations, as it enables individuals to accurately quantify their preferences and values, ultimately leading to better decision-making under uncertainty.
Common Pitfalls to Avoid in Expected Utility Calculations
When calculating expected utility, individuals often make mistakes that can lead to inaccurate results and poor decision-making. One common pitfall is ignoring probability, which can result in overestimating or underestimating the expected utility of an outcome. Another mistake is misestimating utility, which can occur when individuals fail to accurately quantify their preferences and values. Additionally, individuals may fall victim to cognitive biases, such as confirmation bias or anchoring bias, which can influence their probability assignments and utility estimates. To avoid these errors, it is essential to carefully consider each component of the expected utility formula and ensure that probabilities and utilities are accurately estimated. Furthermore, individuals should be aware of their own biases and take steps to mitigate their impact. For instance, using decision analysis tools or seeking input from others can help individuals identify and overcome biases. By understanding how to calculate expected utility and avoiding common pitfalls, individuals can make more informed decisions and achieve better outcomes. In fact, mastering expected utility calculations can help individuals develop a more systematic approach to decision-making, leading to increased confidence and improved decision quality.
Expected Utility in Everyday Life: Applications and Implications
Expected utility calculations have far-reaching implications in various aspects of everyday life, from personal finance to healthcare and business decision-making. In personal finance, understanding how to calculate expected utility can help individuals make informed investment decisions, such as choosing between different asset classes or evaluating the potential returns of a retirement portfolio. In healthcare, expected utility can be used to evaluate the effectiveness of different medical treatments, taking into account the probability of success, potential side effects, and individual preferences. In business, expected utility can inform strategic decisions, such as investing in new projects or evaluating the potential returns of different marketing strategies. Moreover, expected utility can be applied to everyday decisions, such as choosing a career path, selecting a college major, or deciding whether to pursue a new business venture. By applying expected utility calculations to these decisions, individuals can make more informed choices that align with their preferences and values. Furthermore, understanding how to calculate expected utility can also help individuals develop a more systematic approach to decision-making, leading to increased confidence and improved decision quality. As a result, mastering expected utility calculations can have a significant impact on an individual’s overall well-being and success.
Conclusion: Making Informed Decisions with Expected Utility
In conclusion, mastering expected utility calculations is a crucial skill for making informed decisions in various aspects of life. By understanding how to calculate expected utility, individuals can systematically evaluate different options, taking into account the probability of each outcome and its corresponding utility. This framework provides a structured approach to decision-making, enabling individuals to make choices that align with their preferences and values. Moreover, expected utility calculations can help individuals develop a deeper understanding of their own preferences and values, leading to more confident and informed decision-making. By applying expected utility calculations to real-world scenarios, individuals can make better decisions in personal finance, healthcare, and business, ultimately leading to improved outcomes and increased success. Remember, learning how to calculate expected utility is a valuable skill that can be applied to a wide range of decision-making contexts, and by mastering this framework, individuals can unlock decision-making confidence and achieve their goals.